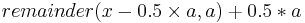We have moved to https://dokuwiki.librecad.org/
Lots of content was already moved to the new wiki, but there is still work to do. If you want to contribute, please register a new account at https://dokuwiki.librecad.org/
This wiki will be kept for a while to keep search engine results valid. Moved sites may be deleted here in future.
Difference between revisions of "Math bits"
R. van Twisk (Talk | contribs) |
(→modular function in LibreCAD) |
||
| Line 1: | Line 1: | ||
| + | == The nearest point on an ellipse to a given point == | ||
| + | An ellipse in the coordinates orientated alone its major and minor axes is given as, | ||
| + | |||
| + | <math> | ||
| + | \begin{cases} | ||
| + | \begin{array}{c} | ||
| + | x=a\cos t\\ | ||
| + | y=b\sin t | ||
| + | \end{array} & 0\le t<2\pi\end{cases} | ||
| + | </math> | ||
| + | |||
| + | The squared distance from a point on ellipse to a given point<math>(x,y)</math>, | ||
| + | |||
| + | <math> | ||
| + | \begin{array}{rcl} | ||
| + | s^{2}&=&(x-a\cos t)^{2}+(y-b\sin t)^{2}\\ | ||
| + | &=&x^{2}+y^{2}+a^{2}\cos^{2}t+b^{2}\sin^{2}t-2xa\cos t-2yb\sin t | ||
| + | \end{array} | ||
| + | </math> | ||
| + | |||
| + | The stationary points at the zero points of its first order derivative of <math>t</math>, | ||
| + | |||
| + | <math> | ||
| + | \frac{d(s^{2})}{dt}=-a^{2}\sin2t+b^{2}\sin2t+2xa\sin t-2yb\cos t=0 | ||
| + | </math> | ||
| + | |||
| + | This stationary condition is a quartic equation of <math>\cos t</math>. With variable change <math> u = \cos t</math>, | ||
| + | |||
| + | <math> | ||
| + | \gamma^{2}u^{4}-2\alpha\gamma u^{3}+(\alpha^{2}+\beta^{2}-\gamma^{2})u^{2}+2\alpha\gamma u-\alpha^{2} = 0 | ||
| + | </math> | ||
| + | |||
| + | where <math>\alpha=2 a x</math>, <math> \beta=2 b y</math>, and <math>\gamma=2(a^2-b^2)</math>. | ||
| + | |||
| + | For all solutions from the quartic equation, the minimum distance point is identified the convex condition, | ||
| + | |||
| + | <math> | ||
| + | \frac{d^{2}(s^{2})}{dt^{2}}=\gamma(1-2u^{2})+\alpha u+\frac{\beta^{2}u}{\alpha-\gamma u}>0 | ||
| + | </math> | ||
| + | |||
== modular function in LibreCAD == | == modular function in LibreCAD == | ||
the standard glibc fmod(x, a) is not convenient here, since we need a modular function work the same way for both positive and negative numbers, instead, we use, | the standard glibc fmod(x, a) is not convenient here, since we need a modular function work the same way for both positive and negative numbers, instead, we use, | ||
Revision as of 23:02, 22 April 2012
The nearest point on an ellipse to a given point
An ellipse in the coordinates orientated alone its major and minor axes is given as,
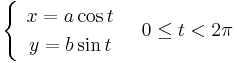
The squared distance from a point on ellipse to a given point(x,y),
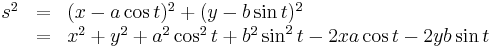
The stationary points at the zero points of its first order derivative of t,
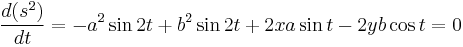
This stationary condition is a quartic equation of cos t. With variable change u = cos t,
γ2u4 − 2αγu3 + (α2 + β2 − γ2)u2 + 2αγu − α2 = 0
where α = 2ax, β = 2by, and γ = 2(a2 − b2).
For all solutions from the quartic equation, the minimum distance point is identified the convex condition,
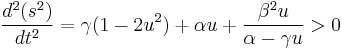
modular function in LibreCAD
the standard glibc fmod(x, a) is not convenient here, since we need a modular function work the same way for both positive and negative numbers, instead, we use,
remainder(x - 0.5*a,a)+0.5*a